[Coding030] 图 - 图的着色

k-图着色

More coding records

Get the knowledge flowing and circulating! :)

目录

标题：图的着色问题

概念

无向图

图着色问题（Graph Coloring Problem，GCP），又称着色问题，是最著名的NP-完全问题之一。

给定一个无向图$G=(V,E)$$G=(V,E)$，其中 $V$$V$ 为顶点集合，$E$$E$ 为边集合，图着色问题即为将 $V$$V$ 分为 $K$$K$ 个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的 $K$$K$ 值。

道路着色问题（Road Coloring Problem）是图论中最著名的猜想之一。

参考：维基百科

相关问题

• 图的 $m$$m$ -着色判定问题——给定无向连通图 $G$$G$ 和 $m$$m$ 种不同的颜色。用这些颜色为图 $G$$G$ 的各顶点着色，每个顶点着一种颜色，是否有一种着色法使 $G$$G$ 中任意相邻的 $2$$2$ 个顶点着不同颜色？

• 图的 $m$$m$ -着色优化问题——若一个图最少需要 $m$$m$ 种颜色才能使图中任意相邻的 2 个顶点着不同颜色，则称这个数 $m$$m$ 为该图的色数。求一个图的最小色数 $m$$m$ 的问题称为 $m$$m$ -着色优化问题。

相关术语

1. 图色数（英语：chromatic number），也被称为顶点色数（vertex chromatic number）：指将一张图上的每个顶点染色，使得相邻的两个点颜色不同，最小需要的颜色数。最小染色数用 ${\displaystyle \chi (G)}$${\displaystyle \chi (G)}$ 或 ${\displaystyle \gamma (G)}$${\displaystyle \gamma (G)}$ 表示。

2. 边色数（edge chromatic number）：指将一张图上的每条边染色，使有公共顶点的边颜色不同，最少需要的颜色数叫边色数，用 ${\displaystyle {\chi }^{\prime }(G)}$${\displaystyle \chi '(G)}$ 表示。

通俗说法

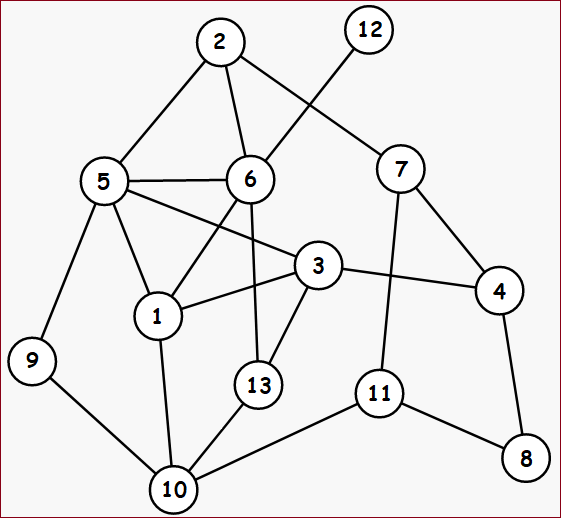
问题1 $m$$m$-着色判定问题

给定一个图 $G$$G$ ，给定一个 $m$$m$ 种颜色，有没有一个方案能够让图 $G$$G$ 中的任意相邻顶点的颜色不一样？

• 有没有？（True or False）

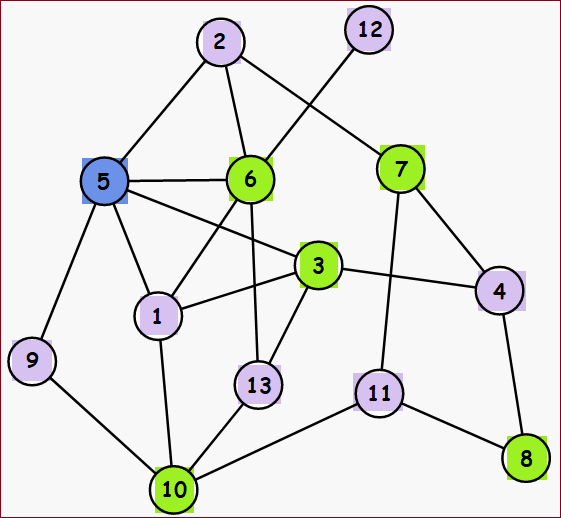
原图	方案1

问题2 $m$$m$-着色判定问题拓展

给定一个图 $G$$G$ ，给定一个 $m$$m$ 种颜色，有多少方案能够让图 $G$$G$ 中的任意相邻顶点的颜色不一样？

• 有多少？（How many）

从这个拓展问题可知，$m$$m$-着色的答案不唯一。

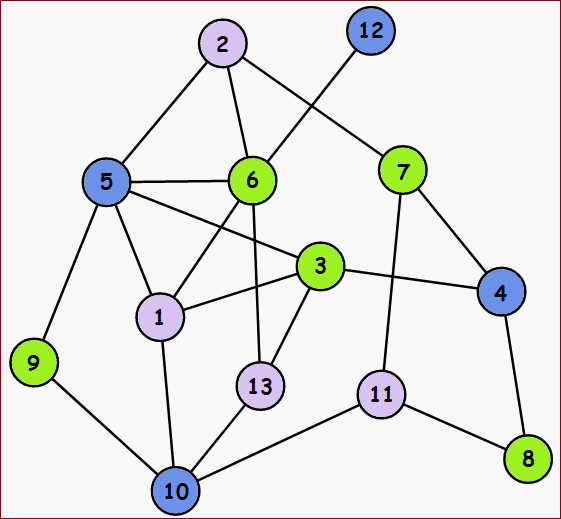
原图	方案1	方案2

问题3 m-着色优化问题

给定一个图 $G$$G$ ，若该图至少需要 $m$$m$ 种颜色才能够让图 $G$$G$ 中的任意相邻顶点的颜色不一样，问这个 $m$$m$ 是多少？

• $m$$m$ 是多少？

代码

问题1

代码 - $m$$m$-着色判定问题

xxxxxxxxxx
75
1
#include<iostream>
2
#include<cstring>
3
using namespace std;
4

5
const int maxn = 105;
6

7
int G[maxn][maxn];
8
int color[maxn];
9

10
// ans 表示是否存在方案[0：不存在；1：存在]。 
11
bool ans; // ans如果是1，则表示对于图G，可以用m种颜色着色，使G中每条边的2个顶点着不同颜色。 
12

13
// n：顶点数
14
// m：颜色数
15
// k：边数 
16
int n, m, k;
17

18
void init()
19
{
20
    ans = 0;  // 初始时，表示不存在这样的方案。 
21
    memset(G, 0, sizeof G);
22
    memset(color, 0 , sizeof color);
23
}
24

25
void dfs(int cur)
26
{
27
    if(cur > n)
28
    {
29
        ans = 1;
30
        return;
31
    }
32
    for(int i = 1; i <= m; i++)  // 对cur结点尝试使用每一种颜色进行涂色
33
    {
34
        bool flag = 1;
35
        // cur之前的结点必被涂色
36
        for(int j = 1; j < cur; j++)
37
        {
38
            if(G[j][cur] == 1 && color[j] == i)
39
            {
40
                flag = 0;  // 只要有一个冲突都不行
41
                break;
42
            }
43
        }
44
        // 如果可以涂上i颜色，则考虑下一个结点的情况
45
        if(flag)
46
        {
47
            color[cur] = i;  // 涂上颜色
48
            dfs(cur + 1);
49
        }
50
        else // 如果到这一步第cur个结点无法着色，则返回探寻其他方案
51
        {
52
            color[cur] = 0;  // 擦除颜色（回溯）;
53
        }
54
    }
55

56
}
57

58

59
int main()
60
{
61
    // 可以一个窗口输入多组数据 
62
    while(cin>>n>>k>>m)
63
    {
64
        init();
65
        for(int i = 1; i <= k; i++)
66
        {
67
            int s, e;
68
            cin>>s>>e;
69
            G[s][e] = G[e][s] = 1;  // 无向图（对称） 
70
        }
71
        dfs(1);
72
        cout<<ans<<endl;  // 输出 0 | 1 
73
    }
74
    return 0;
75
}

问题2

代码 - $m$$m$-着色判定问题（拓展）

xxxxxxxxxx
107
1
#include<iostream>
2
#include<cstring>
3
using namespace std;
4

5
const int maxn = 105;
6

7
int G[maxn][maxn];
8
int color[maxn];
9

10

11
// 图着色判断问题（拓展） 
12
// ans 表示存在多少种方案
13
int ans;
14

15
// n：顶点数
16
// m：颜色数
17
// k：边数 
18
int n, m, k;
19

20
void init()
21
{
22
    ans = 0;  // 初始时默认为没有方案。 
23
    memset(G, 0, sizeof G);
24
    memset(color, 0 , sizeof color);
25
}
26

27
void dfs(int cur)
28
{
29
    if(cur > n)
30
    {
31
        ans = ans + 1;  // 找到1种，就加1 
32
        return;
33
    }
34
    for(int i = 1; i <= m; i++)  // 对cur结点尝试使用每一种颜色进行涂色
35
    {
36
        bool flag = 1;
37
        // cur之前的结点必被涂色
38
        for(int j = 1; j < cur; j++)
39
        {
40
            if(G[j][cur] == 1 && color[j] == i)
41
            {
42
                flag = 0;  // 只要有一个冲突都不行
43
                break;
44
            }
45
        }
46
        // 如果可以涂上i颜色，则考虑下一个结点的情况
47
        if(flag)
48
        {
49
            color[cur] = i; // 涂上颜色
50
            dfs(cur + 1);
51
            color[cur] = 0;  // 擦除颜色（回溯）
52
        }
53
    }
54

55
}
56

57
void dfs2(int cur)
58
{
59
    if(cur > n)
60
    {
61
        ans = ans + 1;  // 找到1种，就加1 
62
        return;
63
    }
64
    for(int i = 1; i <= m; i++)  // 对cur结点尝试使用每一种颜色进行涂色
65
    {
66
        color[cur] = i;  // 涂上颜色（先涂了再说）
67
        
68
        int flag = 1;
69
        // cur和其他节点的涂色情况检查
70
        for(int j = 1; j <= n; j++)
71
        {
72
            if(G[j][cur] == 1 && color[j] == i)
73
            {
74
                flag = 0;  // 只要有一个冲突都不行
75
                break;
76
            }
77
        }
78
        // 如果可以涂上i颜色，则考虑下一个结点的情况
79
        
80
        // 如果检查通过，则flag还是1（没有进入上面for循环里的if语句）
81
        // 如果检查没通过，则flag肯定是0了（下面这句if就不执行了）
82
        if(flag)  
83
        {
84
            dfs2(cur + 1);
85
        }
86
        
87
        color[cur] = 0;  // 擦除颜色（回溯）
88
    }
89
}
90

91
int main()
92
{
93
    // 可以一个窗口输入多组数据 
94
    while(cin>>n>>k>>m)
95
    {
96
        init();
97
        for(int i = 1; i <= k; i++)
98
        {
99
            int s, e;
100
            cin>>s>>e;
101
            G[s][e] = G[e][s] = 1;  // 无向图（对称） 
102
        }
103
        dfs(1);  //dfs2(1)，测试第2种代码（思路更清晰）
104
        cout<<ans<<endl;  // 输出总方案数 
105
    }
106
    return 0;
107
}

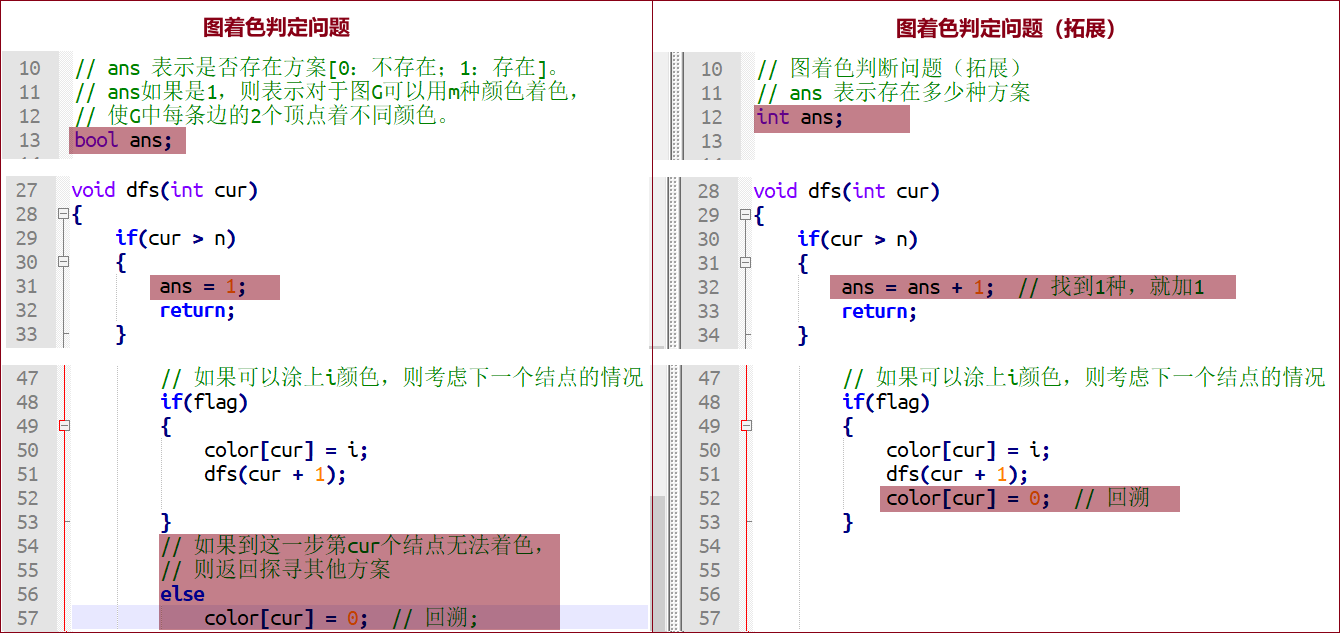
※ 代码对比（图着色判定问题 v.s 图着色判定问题(拓展)）

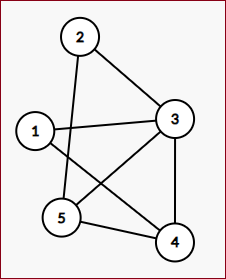
测试样例01

• 5个顶点：编号从1~5

• 7条边

• 3种颜色：红、绿、蓝

注意：顶点编号从1开始，不是从0开始。

输出：6

xxxxxxxxxx
8
1
5 7 3 
2
1 2 
3
2 3 
4
3 4 
5
4 5 
6
5 1 
7
1 3 
8
1 4 

测试样例02

• 13个顶点：编号从1~13

• 41条边

• 3种颜色：红、绿、蓝

注意：顶点编号从1开始，不是从0开始。

输出：336

xxxxxxxxxx
42
1
13 41 3
2
1 3
3
1 5
4
1 6
5
1 10
6
2 5
7
2 6
8
2 7
9
3 1
10
3 4
11
3 5
12
3 13
13
4 7
14
4 8
15
5 1
16
5 2
17
5 3
18
5 6
19
5 9
20
6 1
21
6 2
22
6 5
23
6 12
24
6 13
25
7 2
26
7 4
27
7 11
28
8 4
29
8 11
30
9 5
31
9 10
32
10 1
33
10 9
34
10 11
35
10 13
36
11 7
37
11 8
38
11 10
39
12 6
40
13 3
41
13 6
42
13 10

※ 测试样例03

xxxxxxxxxx
8
1
5 7 3
2
1 3
3
1 4
4
2 3
5
2 5
6
3 4
7
3 5
8
4 5

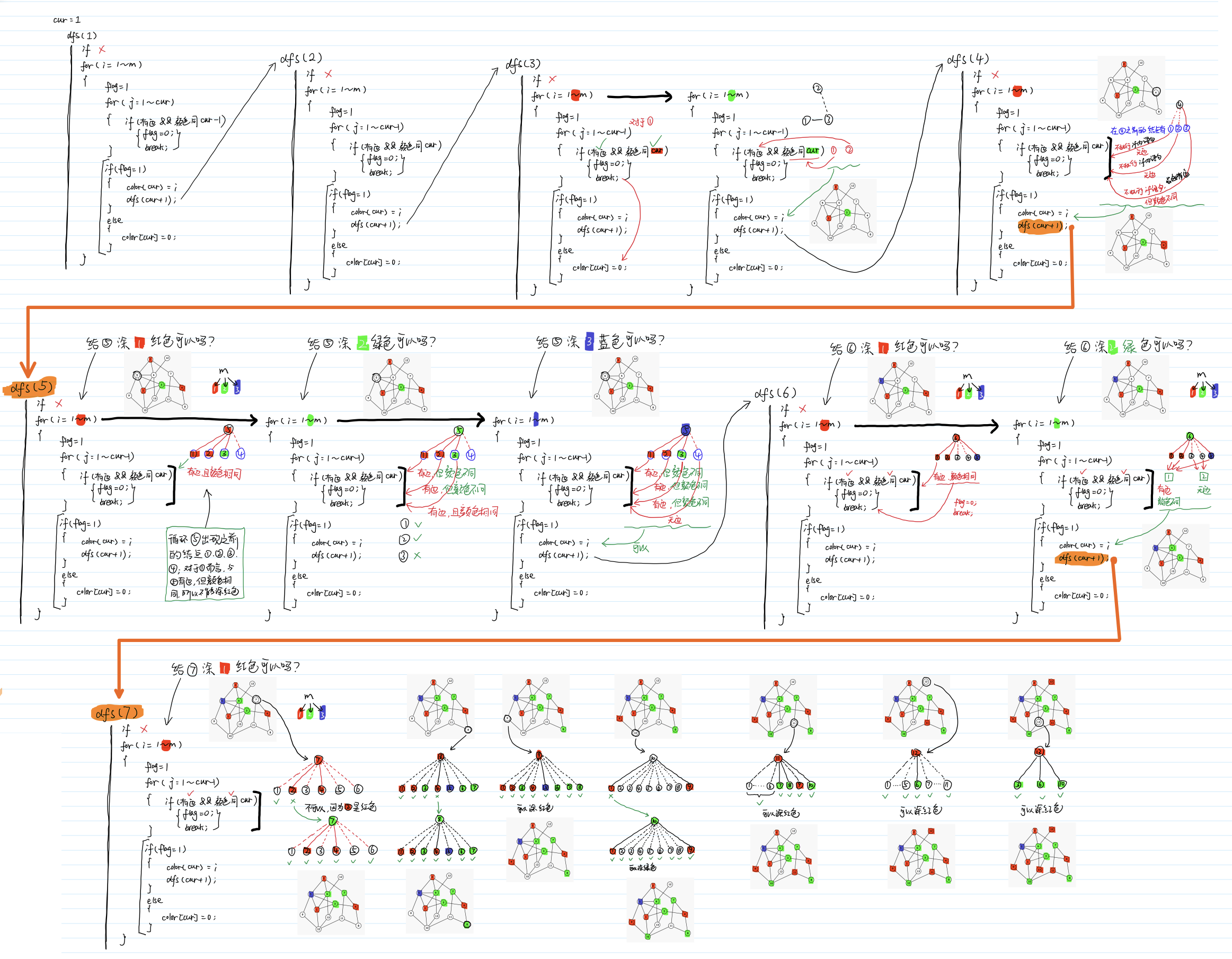
手绘过程示意图

针对void dfs(int cur) 和 测试样例2的过程示意图（输出1种着色方案）

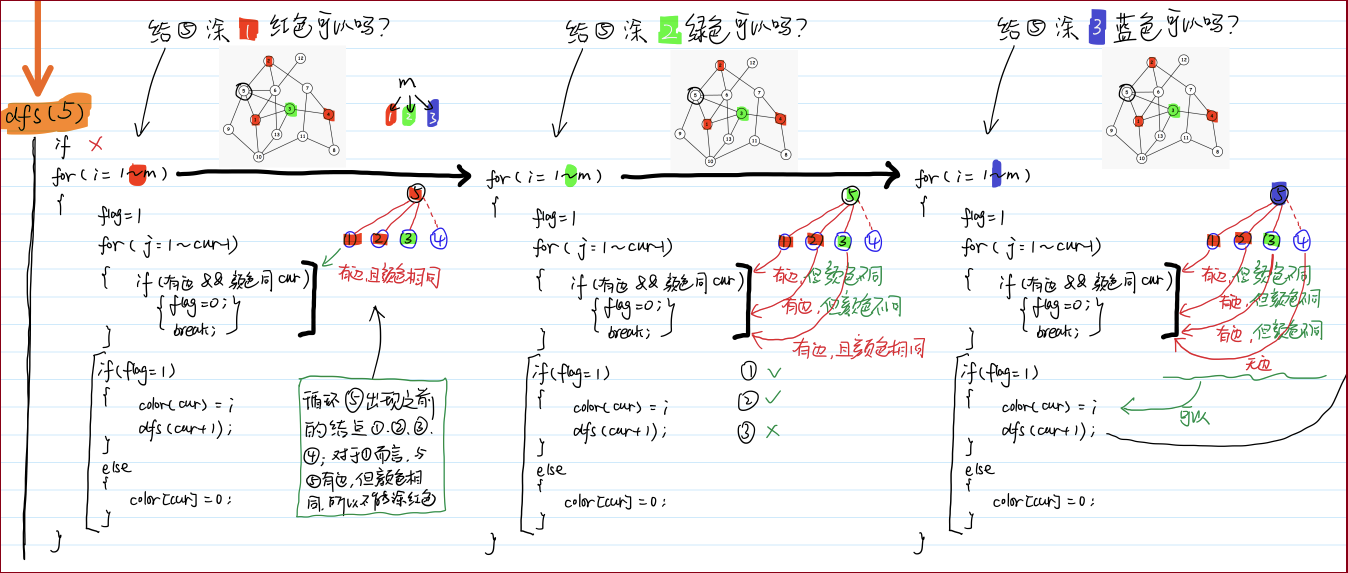
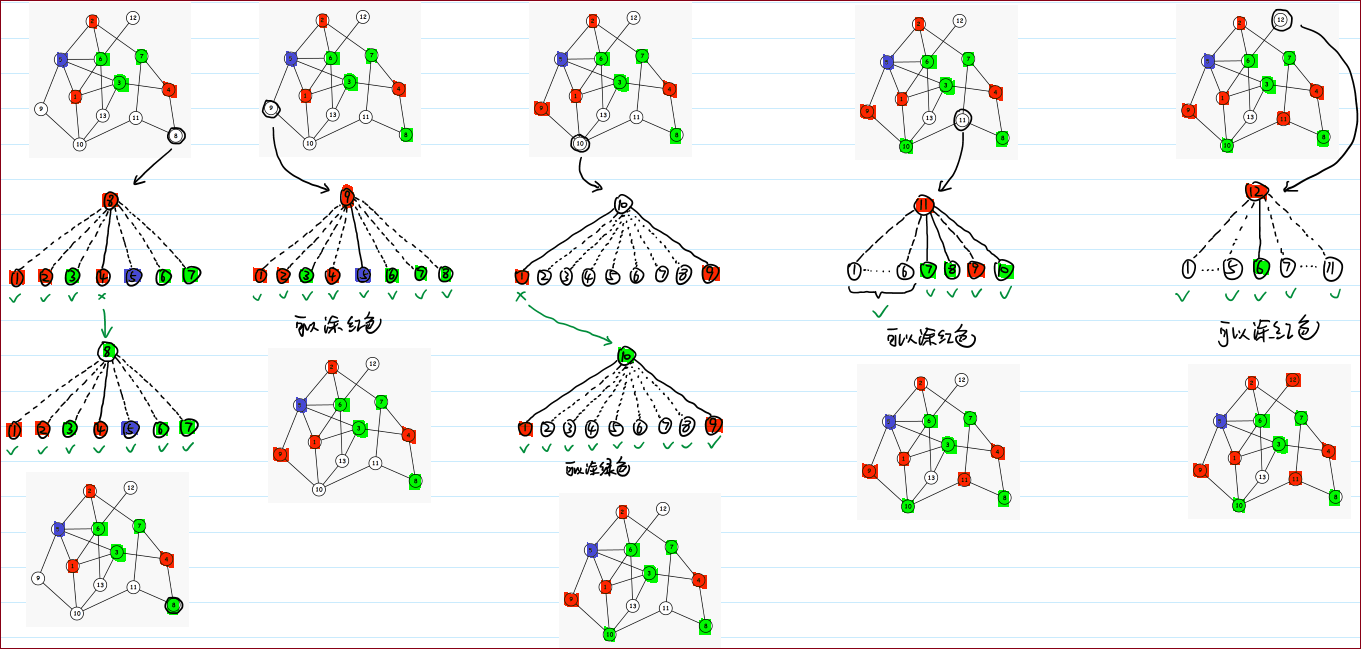
※ 思考 - 如何建模？

条件：元素=[1,2,3,4,5,6,7,8,9]，互斥=[(1,4),(2,5),(1,5),(5,6),(7,8),(3,9),(2,8),(4,5)]

要求：把元素组成 $N$$N$ 个组, 保证互斥元素不在同一个组里, 并且 $N$$N$ 最小。

思路：这个问题实际上就是图的 $m$$m$-可着色优化问题。

参考资料

https://blog.csdn.net/qq_17550379/article/details/102563756

• https://www.cnblogs.com/czsharecode/p/10558732.html

https://blog.csdn.net/Wu_L7/article/details/125062506

https://oi-wiki.org/graph/color/

https://baike.baidu.com/item/%E5%9B%BE%E7%9D%80%E8%89%B2%E9%97%AE%E9%A2%98/8928655